Piscinas de Bolas

As piscinas de bolas são uma forma divertida e segura de entretenimento para crianças. No entanto, é importante seguir algumas recomendações de segurança para garantir a segurança dos utilizadores.

Recomendações de Segurança (ROSPA)

Segundo a ROSPA (Royal Society for the Prevention of Accidents), recomenda-se que piscinas de bolas tenham uma profundidade máxima para reduzir o risco de acidentes por ocultação:

• 450 mm em áreas para crianças pequenas (toddlers)
• 600 mm em áreas para crianças maiores (junior)

 

Não se deve entrar diretamente numa piscina de bolas a partir de um escorrega.

As bolas devem ter um diâmetro mínimo de 70 mm para evitar risco de asfixia.

A superfície da piscina de bolas deve ter uma base nivelada e contínua.

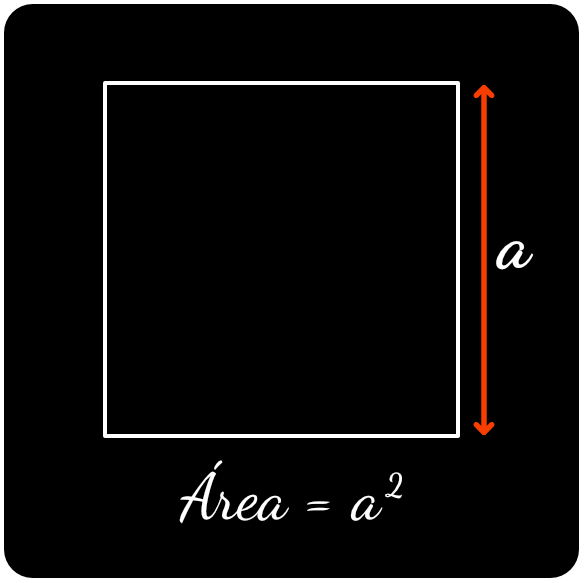
Superfícies com Empacotamento de Círculos – Cálculos em 2D

O empacotamento de círculos é uma disposição de círculos que não se sobrepõem dentro de um espaço delimitado. Este conceito aplica-se a qualquer situação em que bolas fiquem pousadas sobre uma superfície plana, como tanques, piscinas ou reservatórios.

Em geometria, o empacotamento de círculos é uma disposição de círculos que não se sobrepõem dentro de um espaço delimitado e aplica-se a qualquer situação em que bolas fiquem pousadas sobre uma superfície plana, como tanques, piscinas ou reservatórios. A densidade de empacotamento associada corresponde à proporção da superfície coberta pelos círculos.

No espaço bidimensional, Joseph Louis Lagrange provou em 1773 que a disposição de círculos com maior densidade é o empacotamento hexagonal, em que os centros dos círculos estão organizados numa malha hexagonal (linhas desencontradas, como num favo de mel), e cada círculo é rodeado por 6 outros. A densidade deste arranjo é:

Densidade = (π√3)/6 ≈ 90,690%

Utilizando esta percentagem de densidade de 90,7%, é relativamente simples dividir a área de um círculo pela área da superfície que se pretende cobrir e aplicar a densidade de empacotamento para obter um cálculo bastante preciso do número de bolas necessário.

Note-se que este cálculo não considera as bolas “parciais” nas extremidades nem as interrupções no padrão hexagonal, mas em áreas maiores o erro resultante é inferior a 1%.

Empacotamento de Esferas em Volume – Cálculos 3D

O empacotamento de esferas é a disposição de esferas que não se sobrepõem dentro de um determinado espaço. Em espaço tridimensional, existem três tipos de empacotamento para esferas idênticas: grelha cúbica, grelha cúbica com face centrada e grelha hexagonal.

Carl Friedrich Gauss provou, em 1831, que o empacotamento hexagonal é o mais denso possível entre todos os empacotamentos em grelha, com a seguinte fórmula:

Densidade = π / (3 × √2) ≈ 74,048%

Embora a melhor densidade teórica possível seja de cerca de 74%, o pior caso ronda os 60% — abaixo disso, deixa-se de preencher verdadeiramente o espaço ou ignora-se a ação da gravidade. A eficiência típica de empacotamento de esferas despejadas aleatoriamente (como em piscinas de bolas) é de aproximadamente 64%, valor tradicionalmente usado para cálculos com bolas de recreio.

Tal como no cálculo de empacotamento 2D, é relativamente fácil dividir o volume de uma esfera pelo volume do espaço a preencher e multiplicar pela eficiência de 64%, obtendo uma estimativa bastante rigorosa do número de bolas necessárias.